Stanford Machine Learning Note
2015-04-07
课程地址：Machine Learning
单变量线性回归
建立模型
课程里面给的栗子是根据已有的数据集m通过房间面积预测房屋售价。首先建立一个假设，它的输入是房屋的面积x，然后输出是预测的价格y，然后定义这个假设(Hypothesis)为
hθ(x)=θ0+θ1x准则函数
之前已经定义了一个假设函数hθ(x)，现在的目的是要找出一条直线能够很好地拟合数据集m，也就是要找到最合适的θ0和θ1 使它 的hθ(x)值和数据集m中的y值很接近。(x(i),y(i))表示的是样本集m中的第i组数据，所以就可以定义如下的准则函数：
J(θ0,θ1)=12mm∑i=1(hθ(x(i))−y(i))2目标是找到合适的θ0和θ1 使J(θ0,θ1)最小，其实里面的那个2要不要都可以的，除以2是为了后面求导比较方便。然后准则函数叫做均方误差函数，它的的图像是一个平滑的碗状图像，有全局最优解，求这个解的话就要用到梯度下降法了
梯度下降法
学过高数都知道，梯度方向是函数增长最快的方向，那么负梯度方向就是函数下降最快的方向。对于栗子：
Function:J(θ0,θ1)步骤如下：
- 从任意一个点(θ0,θ1)开始，可以取(0,0)
- 改变θ0,θ1的值，使J(θ0,θ1)越来越小，直到收敛
但是呢，根据初始值选取的不同，可能只会得到局部最优解，这个问题的话，后面再讲。 而对于每次迭代的值的更新，使用梯度下降法就是
θj=θj−α∂∂θjJ(θ0,θ1)j=0,1其中α是每次迭代的步长，扩展开就是：
temp0=θ0−α∂∂θ0J(θ0,θ1)其中，如果α太小的话，收敛速度会很慢，如果太大的话可能不会收敛，而且，也没有必要动态地修改α，因为随着迭代，每次减小的步长会越来越小。
对于目标函数J(θ0,θ1)，有：
θ0=θ0−α1mm∑i=1(hθ(x(i))−y(i))现在回到之前说到的根据初始值的不同容易收敛到局部最优解的问题。其实，线性回归的准则函数一般都是一个碗状的函数，这种函数叫凸函数，这种函数没有局部最优解，只有一个全局最优解，所以在使用梯度下降法处理这类准则函数的时候不用担心会收敛到局部最优解的问题。
对于这个栗子中使用的算法，又叫做批量梯度下降法(Batch Gradient Descent)，就是说，每一次迭代都会用到训练数据集m的所有数据。对于求解J的最小值有另一种方法Normal Equations，不需要遍历所有训练数据集.
多变量线性回归
之前举的栗子是通过房屋面积预测价格，现在除了面积有了其他的特征，比如房间数量，楼层，屋子的年龄这些特征，所以现在的训练数据集m从一维变成四维的了。这里，使用n表示特征的数量，x(i)表示输入的ith样本，比如在这里x(2)是一个4*1的矩阵，x(i)j表示第i(th)训练样本的第j个特征，在这里j∈[1,4].所以现在的假设就变成了：
hθ(x)=θ0+θ1x1+θ2x2+θ3x3+θ4x4现在扩展到n个特征:
hθ(x)=θ0+θ1x1+θ2x2+⋯+θnxn为了方便，这里定义x0=1.所以上式就可化为
hθ(x)=θTx然后现在准则函数就变成了：
J(θ)=12mm∑i=1(hθ(x(i))−y(i))2梯度下降法
因为每个特征的数据的取值范围不同，所以如果直接拿过来计算肯定是会出现奇怪的事情的，所以在运算之前，得对数据做一下Feature Scalling，也就是把每个特征的数据归一化到相同的区间，一般来说是[−1,1]或者[0,1],这里给个公式：
xi=xi−μixmaxi−xminiμi是这个特征的均值，这个处理出来的范围是[−0.5,0.5]
评价梯度下降法正确运行的一点是随着迭代次数的增加，J(θ)的值是越来越小的。如果算法不能正常工作的话，试着把α减小一点，一般来说，对于α可以从[…,0.001,0.01,0.1,1,…]
Normal Equation
之前使用的梯度下降法是通过迭代不断修改θi直到J(θ)的最优解。而Normal Equation是通过计算直接得到合适的θ值，现在回到之前的栗子：
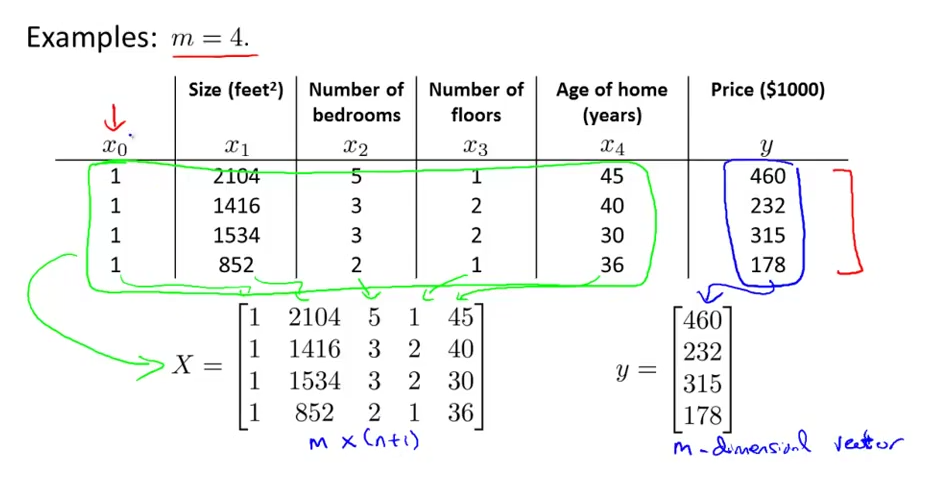如图所示，x0是为了计算方便加的一列，X是m⋅(n+1)特征矩阵,y是每组数据的类标(也就是值),然后用下面的公式可以求解准则函数J(θ)最优解对应的θ值：
那么问题来了，如果XTX是奇异矩阵怎么办？有下面几个办法
- 在matlib和Octave里可以使用pinv(XTX)求解伪逆矩阵
- 去掉样本中冗余的特征(比如x1和x2线性相关)
- 如果m≤n的话，去掉一些特征
然后，对于使用Normal Equation方法求解θ的时候，Feature Scalling是没有必要做的，然是如果使用梯度下降的话，是一定要做Feature Scalling的
对比
现在有m个训练样本，n个特征，什么时候该用梯度下降，什么时候用Normal Equation呢？ 先说一下梯度下降法：
- 优点：n特别大的时候效率很高
- 缺点：需要自己选择α;需要多次迭代
Normal Equation：
- 优点：不需要选择α;不需要迭代
- 缺点：需要计算(XTX)−1比较花时间；n比较大的时候很慢
Logistic Regression
假设现在有一个分类问题：根据肿瘤体积预测它是良性的还是恶性的，如下图的训练样本：
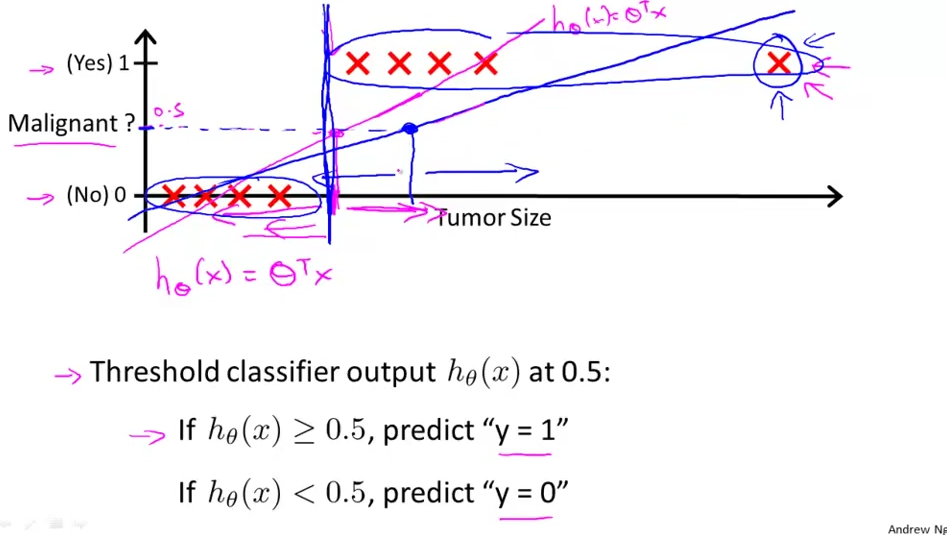上面的一行是恶性肿瘤，下面的一行是良性肿瘤，对于分类问题，如果使用之前的线性回归的话，就不能很好地满足图中的要求，所以一般在这种分类问题中不使用线性回归。
对于一个二分类问题，它的解集永远在{0,1}中，对于线性回归hθ(x)它的值可能>1或者<0，像上图那样。所以引入Logistic Regression：0≤hθ(x)≤1用来处理分类问题
Hypothesis Representation
Want:0≤hθ(x)≤1其中g(z)就是Sigmoid function或者Logistic function,所以Logistic function就变成了：
hθ(x)=11+eθTx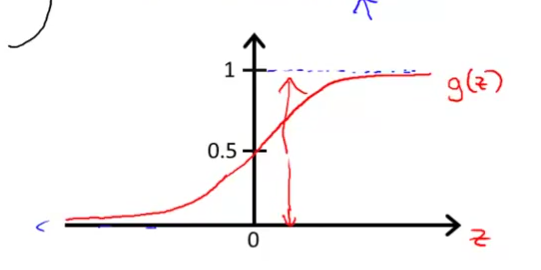
这个就是它的图像了，值域在[0,1]，与y轴的交点是(0,0.5)，满足之前的要求的。
Decision Boundary
首先想下hθ(x)怎样正常工作？
- 当θTx>0的时候，hθ(x)>0.5即y=1
- 当θTx<0的时候，hθ(x)<0.5即y=0
也就是说，需要找到一个判别面把样本集分成两部分，对于复杂的判别面，可能就会用到复杂的多项式来处理了。
准则函数
先说一下目的：现在有m训练样本{(x(1),y(1)),(x(2),y(2)),…,(x(m),y(m))},其中x∈[x0,x1,…,xn]T,x0=1,y∈{0,1},有：
hθ(x)=11+e−θTx现在的问题是，如何选择参数θ?
J(θ)=1mn∑i=1cost(hθ(x(i)),y)这个评价函数的含义就是：如果预测值hθ(x)和真实值y相同的话，评价函数的值就是0，不同的话，评价函数的值就是无穷大。
Simplified Cost Function and Gradient Descent
J(θ)和Cost(hθ(x),y)和上面的一样，而且对于y的值，要么是0要么1,现在对Cost(hθ(x),y)进行简化：
Cost(hθ(x),y)=−ylog(hθ(x))−(1−y)log(1−hθ(x))所以,J(θ)扩展开就变成了下面的样子：
J(θ)=−1m[m∑i=1y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]使用梯度下降法更新求解θ的话：
θ+j=θj−αm∑i=1(hθ(x(i))−y(i))x(i)jAdvanced Optimizetion
比如下面几个
- Conjugate gradient
- BFGS
- L-BFGS
这些算法的优点有：1.不用手动选择α；2.一般来说比梯度下降法要快的。缺点当然也有了，它们都比较复杂。
多分类问题
Regularization
过拟合
过拟合指的是在样本有很多特征的时候，为了追求对训练样本过高的拟合率，建立了复杂的模型去训练，并且训练样本数据拟合地特别特别好，但是对于测试集的效果很糟糕。